2023 杭电多校 7 1008#
HEX-A-GONE Trails
题目大意
给定一棵无根树,两个玩家$(X, Y)$在上面移动,双方只能移动到与自己相邻且没有被任何玩家走过的节点,无法移动的玩家输掉游戏。
题解
首先需要对这个博弈模型进行一些化简,首先我们将 $X, Y$ 之间的路径标记出来,并求出这些路径上的点的价值,这里所谓的价值是以该点为根,不经过 $X, Y$ 路径上的边能够达的点的深度的最大值。例如下面这图能够如此化简:
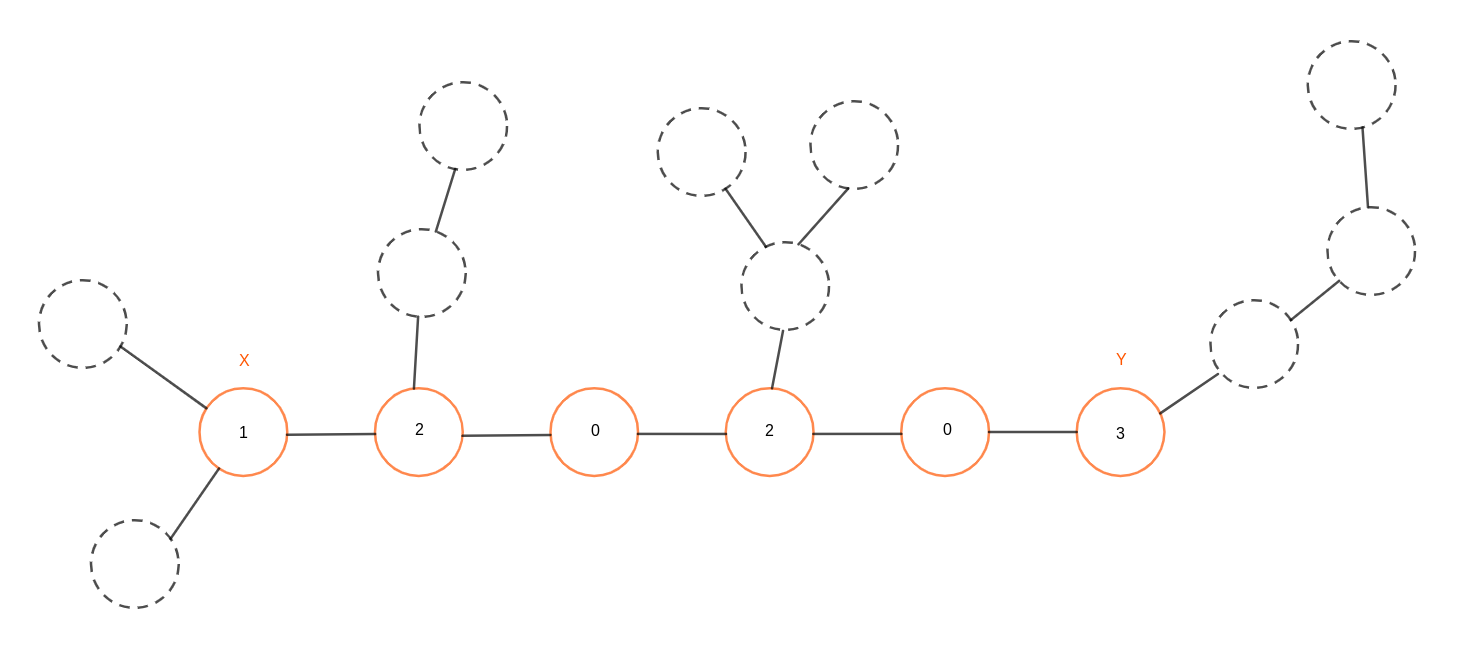
现在用两个指针表示出两个玩家所在的位置,那么可以计算出两个玩家所获得的值(值为所在位置的值加上与初始点的距离的和),以及胜负关系(玩家一获得的值严格大于玩家而获得的值为胜)。
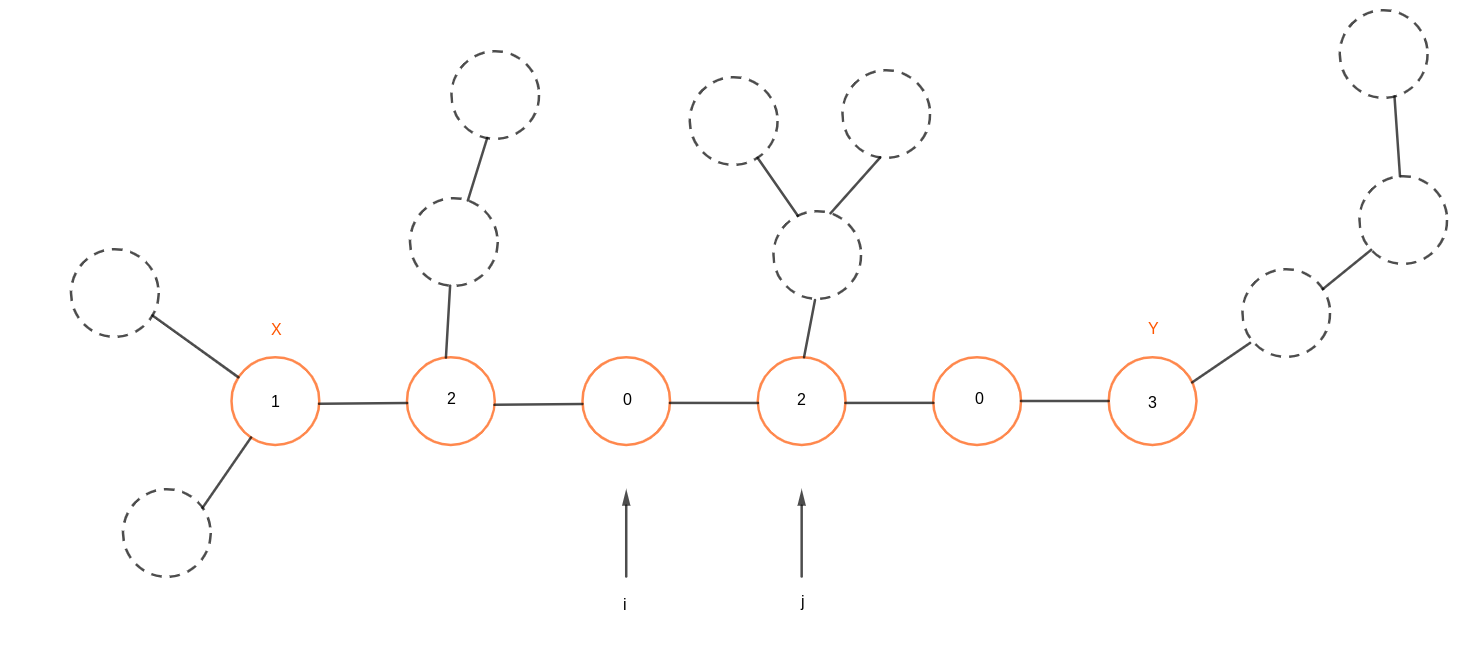
可以用当前局面的胜负关系来判断两个指针的移动方向,例如在上图的状态中,玩家一获得的值显然小于玩家二的值,那么如果玩家一想要胜利,那么 $i$ 指针就必须向靠近 $x$ 初始点的方向移动,那么玩家二的选择实际上就成了一个区间。
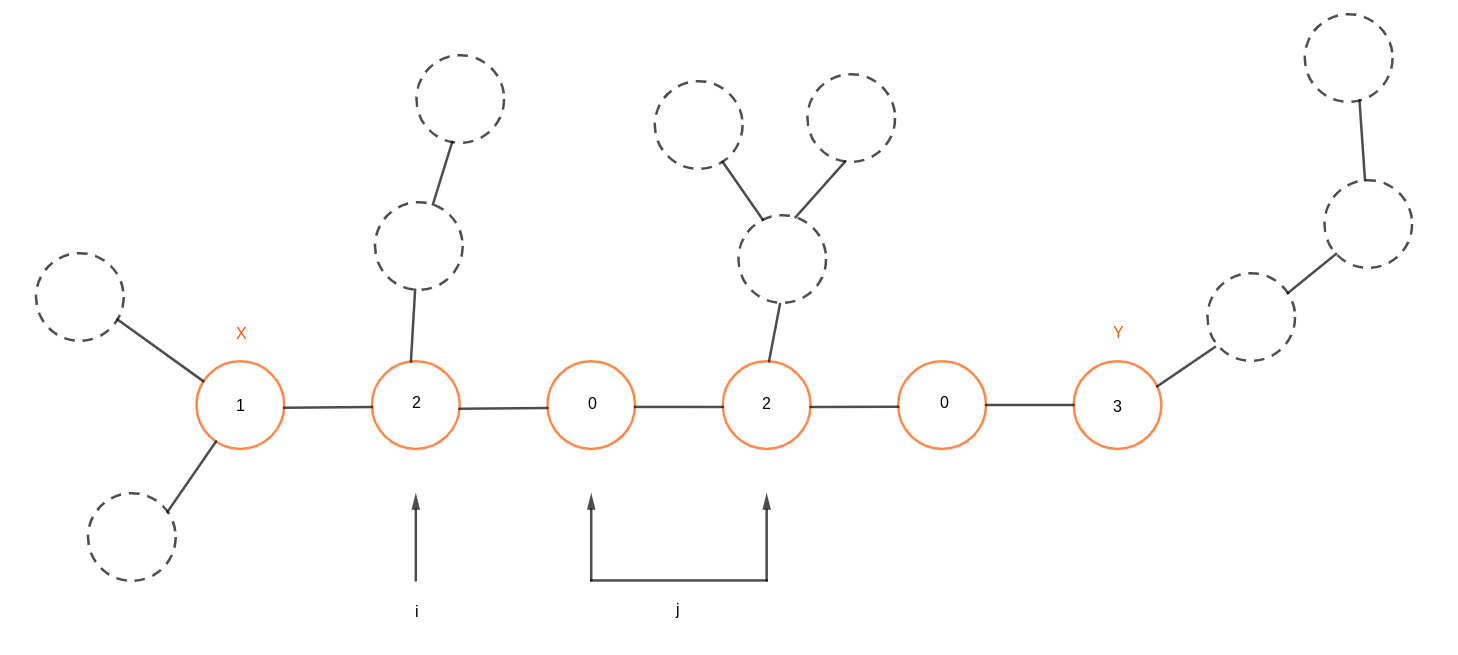
不断重复上述过程,直到两个指针移出被标记的点。
因为对于一个玩家来说,指针到达过的地方不会再次经过,因此可以用链表来维护 $i, j$ 两个指针的前驱和后继,区间的最值可以直接通过前缀得到,不需要数据结构。
时间复杂度 $O(n)$。
参考代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
| void solve() {
int n;
cin >> n;
vector<vector<int>> tre(n);
vector<int> path, col(n);
int x, y;
cin >> x >> y;
x --, y --;
for(int i = 0; i < n - 1; i ++) {
int u, v;
cin >> u >> v;
u --, v --;
tre[u].push_back(v);
tre[v].push_back(u);
}
auto dfs = [&](auto self, int u, int f) -> bool {
if(u == y) {
path.push_back(u), col[u] = true;
return true;
}
for(int v : tre[u]) if(v != f) {
if(self(self, v, u)) {
path.push_back(u), col[u] = true;
return true;
}
}
return false;
};
dfs(dfs, x, x);
reverse(path.begin(), path.end());
int w = path.size();
vector<int> val(n), dep(n);
auto get_v = [&](auto self, int u, int f) -> int {
dep[u] = dep[f] + 1;
int res = 0;
for(auto v : tre[u]) if(v != f && !col[v]) {
res = max(res, self(self, v, u));
}
res ++;
return res;
};
for(int i : path) {
val[i] = get_v(get_v, i, i);
}
int mxx = 0, mxy = 0, curx = 0, cury = w - 1;
for(;curx + 1 < cury;) {
if(curx + 1 < cury) curx ++;
if(cury - 1 > curx) cury --;
}
mxx = val[path[curx]] + curx;
mxy = val[path[cury]] + w - 1 - cury;
bool res = mxx > mxy;
vector<int> nxtA(w, -1), preA(w, -1), nxtB(w, -1), preB(w, -1);
for(int i = 0; i < w - 1; i ++) {
nxtA[i] = i + 1;
preB[i] = i + 1;
}
for(int i = w - 1; i >= 1; i --) {
preA[i] = i - 1;
nxtB[i] = i - 1;
}
auto del =[&] () {
if(nxtA[curx] != - 1) preA[nxtA[curx]] = preA[curx];
if(preA[curx] != - 1) nxtA[preA[curx]] = nxtA[curx];
if(nxtB[cury] != - 1) preB[nxtB[cury]] = preB[cury];
if(preB[cury] != - 1) nxtB[preB[cury]] = nxtB[cury];
};
while(cury != -1 && curx != -1) {
if(res) {
del();
curx = nxtA[curx];
cury = preB[cury];
if(cury == -1) {
break;
}
mxx = max(mxx, val[path[curx]] + curx);
mxy = val[path[cury]] + w - 1 - cury;
} else {
del();
cury = nxtB[cury];
curx = preA[curx];
if(curx == -1) {
break;
}
mxx = val[path[curx]] + curx;
mxy = max(mxy, val[path[cury]] + w - 1 - cury);
}
res = mxx > mxy;
}
cout << (res ? 1 : 0) << '\n';
}
|
2023 牛客多校 4 H#
Merge the squares!
题目大意
给定一个 $n \times n$ 个 $1 \times 1$ 的小正方形组成的一个大正方形。
要求每次选取不超过 $50$ 个正方形拼接成一个新大正方形,最终需要得到一个 $n \times n$ 的正方形。
输出一种可行的方案。
题解
考虑分治的做法。
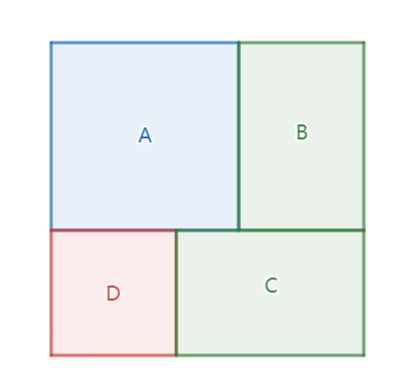
对于一个正方形,可以分割成如下图的形式:
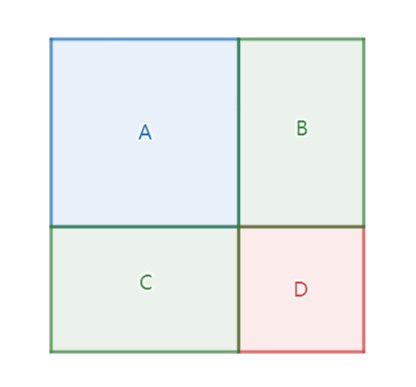
其中 $A, D$ 是两个正方形,$B, C$ 是两个大小相等的矩形。
显然对于正方形 $A, D$ 可以直接递归处理,处理比较棘手的是两个矩形该如何处理。
对于一个矩阵而言,分割成最少的正方形的方案是对其长宽进行辗转相减,那么可以预处理出对于任意一个矩阵能够分成的正方形数量。
我们可以枚举 $B, C$ 的长宽,找到分割最少的矩阵,分治这个矩阵即可。
当然如果确定了矩形的长宽,这四个矩形可以任意摆放,例如另一种等价的摆放方式:
参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
| int g[MAXN][MAXN];
vector<tuple<int, int, int>> res;
int dp(int x, int y) {
if(x == y) {
return g[x][y] = 1;
}
if(g[x][y]) return g[x][y];
if(x > y) {
return g[x][y] = 1 + dp(x - y, y);
} else {
return g[x][y] = 1 + dp(x, y - x);
}
}
void div2(int x1, int y1, int x2, int y2);
void div1(int x1, int y1, int x2, int y2) {
int len = x2 - x1 + 1;
if(len <= 7) {
if(len > 1) {
res.push_back({x1, y1, len});
}
return;
}
int div = 0, mxcnt = INF;
for(int i = 1; i <= len / 2; i ++) {
int x = dp(i, len - i);
if(x < mxcnt) {
mxcnt = x, div = i;
}
}
len = div;
div1(x1, y1, x1 + len - 1, y1 + len - 1);
div1(x1 + len, y1 + len, x2, y2);
div2(x1 + len, y1, x2, y1 + len - 1);
div2(x1, y1 + len, x1 + len - 1, y2);
res.push_back({x1, y1, x2 - x1 + 1});
}
void div2(int x1, int y1, int x2, int y2) {
int lenx = x2 - x1 + 1, leny = y2 - y1 + 1;
if(lenx == 1 || leny == 1) {
return;
}
if(lenx == leny) {
div1(x1, y1, x2, y2);
return;
}
if(lenx > leny) {
div1(x1, y1, x1 + leny - 1, y1 + leny - 1);
div2(x1 + leny, y1, x2, y2);
} else {
div1(x1, y1, x1 + lenx - 1, y1 + lenx - 1);
div2(x1, y1 + lenx, x2, y2);
}
}
void solve() {
int n;
cin >> n;
div1(1, 1, n, n);
cout << res.size() << '\n';
for(auto [x, y, len] : res) {
cout << x << " " << y << " " << len << '\n';
}
}
|
Harmony in Harmony
题目大意: $n$个人将大小为$1$的地均分两次, 第一次每人分得$1/n$, 第二次同样分为大小相同的$n$份, $n$人自行分配, 要求使得第一次和第二次区域的交集最小的人的值最大, 第二次均分地时有一种分法, 使得这个值最小, 求出这个值.
首先可以猜测此题的答案存在一个上界$\frac{1}{n^2}$. 可以将此过程看作一个完全二分图匹配, 我们可以列出一个$n\times n$的表格, 其中每行的值之和为$\frac{1}{n}$, 每列的值之和为$1$, 所求的值为表格中坐标为 $(i, i)$ 的最小值. 我们假定 $(i, i)$ 为我们要找的最小值, 那么为了让这个值最小, 可以让 $\sum_{k = 1}^{i - 1}(k, i)$ 最大, 又因为要让每人分得的土地最大, 可以让前$i-1$个人分得的土地一样大都为$\frac{1}{in}$, 那么$i$分得的土地大小应为$\frac{\frac{1}{n}-\frac{i-1}{in}}{n-i+1}$, 验证此值小于等于$\frac{1}{n^2}$, 故枚举 $i$ 求出答案.
参考代码:
1
2
3
4
5
6
7
8
9
| int main () {
int n;
scanf("%d", &n);
double res = 1;
for(int i = 0; i <= n; i ++) {
res = min(res, 1.0 / (n * (n + 1 - i) * i));
}
printf("%.9f", res);
}
|
Paimon Sorting
题目大意: 给出一种$n^2$的排序方式, 询问数组长度为$k$时, 在排序的过程中交换了几次$k\in [1, n]$.
假设我们已经知道长度为$x$的结果, 那么怎么样可以推出$x + 1$的结果就是此题的关键. 设已经出现的最大值为$mx$, 考虑下面几种情况: $a_x < mx$; $a_x = mx$; $a_x > mx$.
首先考虑第一种情况, 注意到该排序每轮是将最大值交换到$i$位置, 因此对于这种情况只需要考虑最后一轮, 从$1$到$x$位置,每次遇到大于$a_x$的数便交换, 实际交换的次数为大于$a_x$的数的集合的大小.
其次考虑第三种情况, 首先$a_x$会走所有前一个最大值所有经过的路径, 此过程的价值为$0$, 其次$a_x$ 会被移动到$1$位置, 再被移动到$x$位置, 此段的价值为 $2$.
最后考虑第二中情况, 显然它本身的价值应该为$0$, 但是它会对下一个 mx 移动到末位置产生阻碍(增加那一段的价值).这段增量为此时的位置到下一个mx位置的长度.
参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| struct BIT {
int N;
vector<int> c;
BIT(int n) {
N = n;
c.resize(N);
};
void add(int x) {
for(int i = x; i < N; i += (i & (-i))) {
c[i] += 1;
}
}
ll sum(int x) {
ll res = 0;
for(int i = x; i; i -= (i & (-i))) {
res += c[i];
}
return res;
}
ll sum(int l, int r) {
return sum(r) - sum(l - 1);
}
};
void solve() {
int n;
cin >> n;
vector<int> a(n);
for(int i = 0; i < n; i ++) {
cin >> a[i];
}
ll res = 0;
BIT bit(n + 10);
vector<int> tol(n + 1);
int len = -2;
int mx = 0;
for(int i = 0; i < n; i ++) {
if(mx < a[i]) {
res += 2 + len;
mx = a[i];
len = 0;
} else if(mx == a[i]) {
len ++;
} else {
if(len) len ++;
}
res += bit.sum(a[i] + 1, n + 5);
if(!tol[a[i]]) {
tol[a[i]] = 1;
bit.add(a[i]);
}
cout << res;
if(i == n - 1) {
cout << '\n';
} else {
cout << ' ';
}
}
}
|
Exercise
题目大意: 给定$2n$个数, 原本(1, 2), (3, 4) … 是一组, 现在要重新分组, 但不能维持原来的组, 问重新分组后每组两个值差的绝对值和的最小值.
显然从小到大排序之后, 相邻的两个数分为一个组会使得绝对值和最小, 但不一定符合条件, 于是我们希望能通过某种方法使得所有不合法的组都合法.
发现需要被最优的重组方式一定是与相邻的组进行重组, 且增量为$2(p_{i + 1,l} - p_{i,r})$.
可以考虑一种这样的DP, $dp_{i,j}$, 其中$i$表示考虑到第$i$组, $j$表示该组是否需要被重组.
可以写出转移方程:
$$
\begin{matrix}
dp_{i, 1} = dp_{i-1, 0}\
dp_{i, 0} = min(dp_{i-1,0},\ dp_{i,0},\ dp_{i,1} + 2(p_{i + 1,l} - p_{i,r}))
\end{matrix}
$$
参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| const ll INF = (1ll << 60);
struct PAIR {
ll l, r;
bool bad = 0;
};
void solve() {
int n;
cin >> n;
vector<PII> a(2 * n);
for(int i = 0; i < 2 * n; i ++) {
cin >> a[i].first;
a[i].second = i + 1;
}
sort(a.begin(), a.end());
ll res = 0;
vector<PAIR> p(n);
for(int i = 0; i < n; i ++) {
p[i].l = a[2 * i].first;
p[i].r = a[2 * i + 1].first;
res += p[i].r - p[i].l;
int mx = max(a[2 * i].second, a[2 * i + 1].second);
int mi = min(a[2 * i].second, a[2 * i + 1].second);
if(mx - 1 == mi && (mx % 2 == 0)) {
p[i].bad = 1;
}
}
vector<array<ll, 2>> dp(n);
dp[0][0] = dp[0][1] = INF;
dp[0][p[0].bad] = 0;
for(int i = 1; i < n; i ++) {
dp[i][0] = dp[i][1] = INF;
dp[i][p[i].bad] = dp[i - 1][0];
dp[i][0] = min(dp[i][0], min(dp[i - 1][0], dp[i - 1][1]) + 2 * (p[i].l - p[i - 1].r));
}
res += dp[n - 1][0];
cout << res << '\n';
}
|
Fortune over Sportsmanship
题目大意: $n$人参见一个网球比赛, 一个$n\times n$的方格表示$(i, j)$进行比赛时收获的人气, 比赛总共进行$n - 1$轮, 胜方获得败方的人气(二者取max), 且败方淘汰出局.现在希望求出比赛可能收获的人气最大值, 并找出赛程.
考虑一种贪心的过程, 每次使当前状态下人气最大的两名选手进行比赛, 因为会继承败方的人气, 所以无论哪名选手淘汰都没关系. 可以用优先队列来模拟比赛.
参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| struct Z {
int val;
int x, y;
bool operator< (const Z &a) const {
if(val != a.val) {
return val < a.val;
} else {
return x < y;
}
}
};
void solve() {
int n;
cin >> n;
ll res = 0;
vector<vector<int>> p(n, vector<int> (n));
vector<bool> over(n);
vector<PII> op;
for(int i = 0; i < n; i ++) {
for(int j = 0; j < n; j ++) {
cin >> p[i][j];
}
}
priority_queue<Z> q;
for(int i = 0; i < n; i ++) {
for(int j = i + 1; j < n; j ++) {
q.push({p[i][j], i, j});
}
}
while(q.size()) {
int v = q.top().val;
int x = q.top().x;
int y = q.top().y;
q.pop();
if(!over[x] && !over[y]) {
op.push_back({x, y});
res += v;
over[y] = 1;
for(int i = 0; i < n; i ++) {
if(over[i] || i == x) continue;
p[i][x] = p[x][i] = max(p[x][i], p[y][i]);
q.push({p[x][i], min(x, i), max(x ,i)});
}
}
}
cout << res << '\n';
for(auto &[x, y] : op) {
cout << x + 1 << ' ' << y + 1 << '\n';
}
}
|
Gaining Rating
题目大意: Monocarp 想提高自己在某下棋网站上的rating, 希望从$x$上升到$y$. 现在有$n$个对手, 每个对手有相应的rating $a_i$, rating 变化的规则为, 获胜加$1$, 失败减$1$但是对手的rating不变, Monocarp 只能下赢rating不大于自己的对手, 同时他可以自己挑选对手, 但是任意两个对手进行对弈的次数差不能大于$1$. 问需要多少轮才能达到目标或者说是不可能的.
显然, 首先需要对所有对手的rating进行一次排序. 我们考虑模拟一轮获得增量, 首先能够赢过$t$个人, 再败给$n-t$个人, 一轮总共获得的分数为$2t-n$, 如果距离所需达成的最终目标小于等于$t$时, 我们便可以不进入下一轮, 反之, 如果这一轮获得的分数小于等于$0$时, 无论如何都无法达到目标. 我们考虑如何求出$t$, 显然直接对$a$进行upper_bound是错误的, 因为我们的分数是在变化的. 可以考虑维护一个$b_i = a_i - i$表示想一路赢到$i$所需的最小rating. 但是这样的$b$不是单调的, 我们将不单调的$b_i$向下合并, 并增设权值, 这样我们得到了一个可以$log$求出$t$的数组.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| sort(a.begin(), a.end());
vector<ll> b = a;
for(int i = 0; i < n; i ++) {
b[i] -= i;
}
vector<int> s(1, 1);
vector<ll> v(1, b[0]);
for(int i = 1; i < n; i ++) {
if(b[i] <= v.back()) {
s.back() ++;
} else {
v.push_back(b[i]);
s.push_back(1);
}
}
v.push_back(1e18);
for(int i = 1; i < s.size(); i ++) {
s[i] += s[i - 1];
}
|
上述代码中$v$表示所说的单调数组, $s$表示增量, 接下来我们还不能一下子求出最后的答案, 我们将$v$中数值的大小视为分段的分界线, 已经知道了当前一轮所获得的增量, 我们要判断增量发生变化的值与$y-s_i$哪一个先到, 依次模拟每个分段便能求出最后的答案.
参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| void solve() {
int n;
ll x, y;
cin >> n >> x >> y;
vector<ll> a(n);
for(int i = 0; i < n; i ++) {
cin >> a[i];
}
sort(a.begin(), a.end());
vector<ll> b = a;
for(int i = 0; i < n; i ++) {
b[i] -= i;
}
vector<int> s(1, 1);
vector<ll> v(1, b[0]);
for(int i = 1; i < n; i ++) {
if(b[i] <= v.back()) {
s.back() ++;
} else {
v.push_back(b[i]);
s.push_back(1);
}
}
v.push_back(1e18);
for(int i = 1; i < s.size(); i ++) {
s[i] += s[i - 1];
}
for(int i = 1; i < s.size(); i ++) {
s[i] += s[i - 1];
}
ll res = 0;
while(1) {
int i = upper_bound(v.begin(), v.end(), x) - v.begin();
if(!i) {
cout << -1 << '\n';
return ;
}
if(x + s[i - 1] >= y) {
cout << res + y - x << '\n';
return ;
} else {
int add = 2 * s[i - 1] - n;
if(add <= 0) {
cout << -1 << '\n';
return;
} else {
ll ter = min(y - s[i - 1], v[i]);
ll cnt = (teg - x + add - 1) / add;
res += cnt * n;
x += cnt * add;
}
}
}
}
|
https://codeforces.com/contest/1754/problem/F
https://codeforces.com/contest/822/problem/C
https://codeforces.com/contest/229/problem/D
https://codeforces.com/contest/1288/problem/D
https://codeforces.com/gym/104114/problem/G
https://codeforces.com/gym/103446/problem/J
https://codeforces.com/gym/103470/problem/I
https://codeforces.com/gym/103447/problem/G
https://codeforces.com/gym/104023/problem/J
https://codeforces.com/gym/104023/problem/D




